Partie 3 - Du vrai rendu 3D

Charger un mesh depuis un fichier

Pour commencer, nous allons enfin utiliser de vrais modèles 3D. Pour cela, nous allons utiliser la librairie tinyobjloader qui lit le format de fichier .obj (un format simple de modèle 3D, qui est essentiellement une longue liste de sommets avec positions, UVs, normales, etc.). La librairie est déjà inclue par opengl-framework, vous n'avez rien à faire de ce côté là.

Il va nous falloir créer un tableau de floats qu'on va remplir avec les positions, UVs et normales du mesh, et nous allons ensuite utiliser ce tableau comme data pour créer un gl::Mesh :

auto load_mesh(std::filesystem::path const& path) -> gl::Mesh
{
    // On lit le fichier avec tinyobj
    auto reader = tinyobj::ObjReader{};
    reader.ParseFromFile(gl::make_absolute_path(path).string(), {});

    if (!reader.Error().empty())
        throw std::runtime_error("Failed to read 3D model:\n" + reader.Error());
    if (!reader.Warning().empty())
        std::cout << "Warning while reading 3D model:\n" + reader.Warning();

    // On met tous les attributs dans un tableau
    auto vertices = std::vector<float>{};
    for (auto const& shape : reader.GetShapes())
    {
        for (auto const& idx : shape.mesh.indices)
        {
            // Position
            vertices.push_back(reader.GetAttrib().vertices[3 * idx.vertex_index + 0]);
            vertices.push_back(reader.GetAttrib().vertices[3 * idx.vertex_index + 1]);
            vertices.push_back(reader.GetAttrib().vertices[3 * idx.vertex_index + 2]);

            // UV
            vertices.push_back(reader.GetAttrib().texcoords[2 * idx.texcoord_index + 0]);
            vertices.push_back(reader.GetAttrib().texcoords[2 * idx.texcoord_index + 1]);

            // Normale
            vertices.push_back(reader.GetAttrib().normals[3 * idx.normal_index + 0]);
            vertices.push_back(reader.GetAttrib().normals[3 * idx.normal_index + 1]);
            vertices.push_back(reader.GetAttrib().normals[3 * idx.normal_index + 2]);
        };
    }

    // TODO créer et return un gl::mesh, qui utilisera le tableau `vertices` en tant que `data` pour son vertex buffer.
    // Attention, il faudra bien spécifier le layout pour qu'il corresponde à l'ordre des attributs dans le tableau `vertices`.
}

Complétez la fonction ci-dessus pour construire un mesh à partir du tableau de vertices obtenu grâce à tinyobj. Il vous suffit ensuite de remplacer votre mesh de cube par un mesh loadé avec cette fonction, et le tour est joué ! Pour vos tests, vous pouvez utiliser ce modèle 3D et le mettre dans votre dossier res.

astuce

Si votre modèle est penché sur le côté au début, c'est "normal". Il n'y a pas de convention universelle pour l'axe qui pointe vers le haut : certaines utilisent Y, et d'autres Z. Il faudra donc légèrement modifier les vertexs du mesh au moment du loading afin de faire pointer le bon axe vers le haut.

astuce

N'essayez pas de faire un index buffer, les sommets tels qu'ils sont donnés par tinyobjloader ont un index buffer différent pour chaque attribut, ce qui n'est pas supporté par OpenGL. Il faudrait plutôt inspecter tous les sommets pour détecter ceux qui ont les mêmes positions et UVs et normales et recréer notre propre index buffer à partir de ça.

Note

Il y a aussi un fichier .mtl dans le modèle que je vous ai fourni. Il décrit le matériau de l'objet, nous en parlerons plus tard.

Premier modèle d'éclairage et Normales

Normales

Nous allons maintenant commencer à éclairer plus ou moins nos objets en fonction des différentes lumières présentes dans la scène. Tout va se passer dans le fragment shader, qui va être responsable de faire ces calculs pour chaque pixel, et d'atténuer plus ou moins la couleur de base du pixel (appelée albedo) en fonction de la quantité de lumière reçue.

Pour faire ces calculs de lumière, nous avons besoin de connaître l'orientation de notre surface (pour savoir à quel point elle est face à la lumière) et c'est à ça que servent les normales :

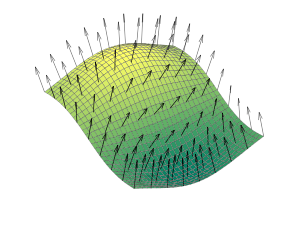
La normale est le vecteur perpendiculaire à la surface ; on pourrait le calculer à la volée en connaissant les trois sommets du triangle, mais il est le plus souvent précalculé et stocké dans le vertex buffer. Par exemple dans le .obj que nous utilisons, les normales sont déjà stockées dans le fichier, en plus des positions et des UVs. Rajoutez les normales dans votre vertex buffer, et dans un premier temps pour vérifier qu'elles sont bonnes, affichez les en tant que couleur de l'objet :

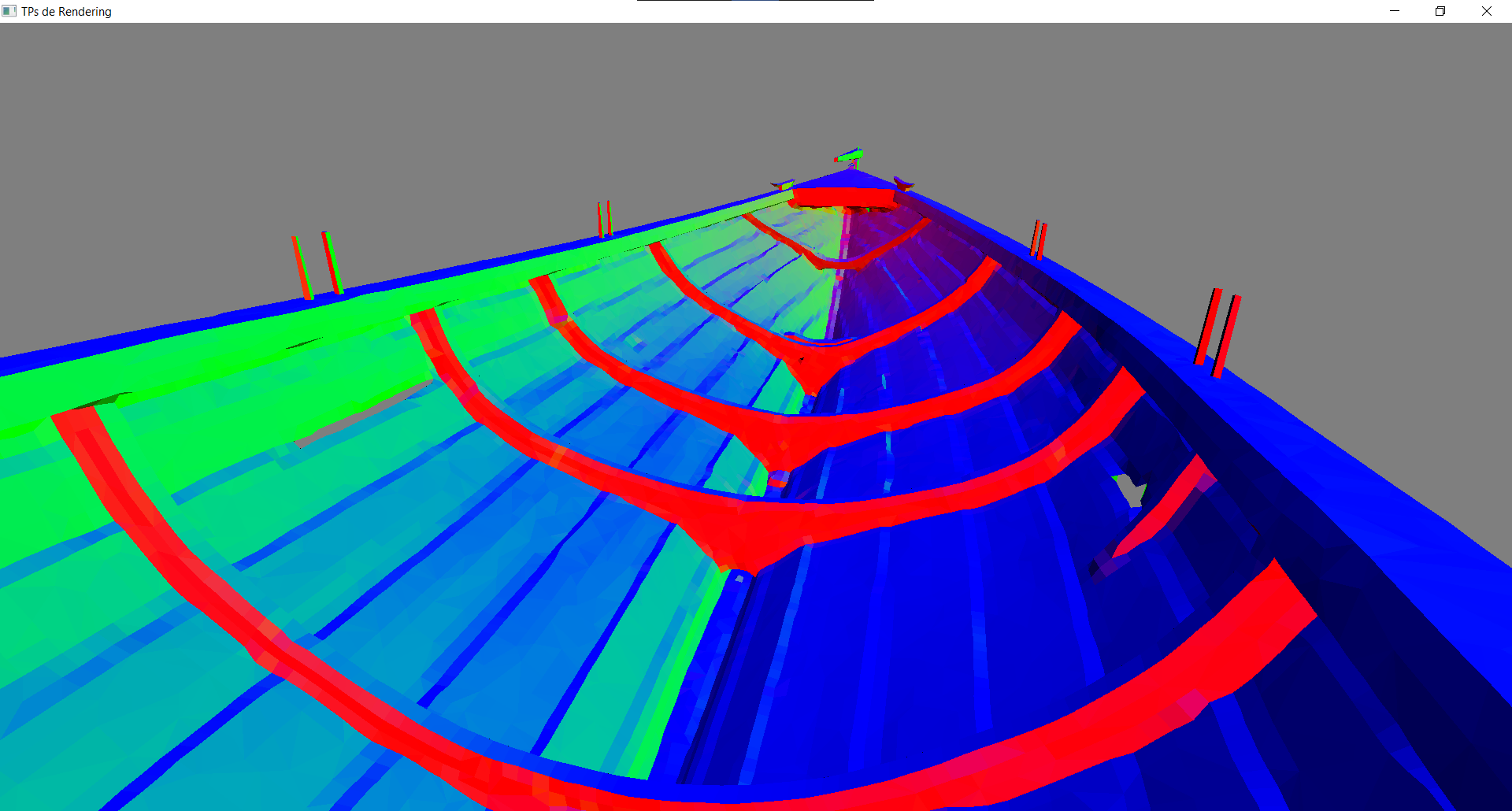
On peut interpréter les couleurs : RGB = XYZ : en bleu ce sont les normales qui pointent vers Z, i.e. vers le haut. En rouge et vert sont celles qui pointent vers X et Y.

Lumière directionnelle

Maintenant il nous faut décrire notre lumière. Nous allons commencer par le type le plus simple, les lumières directionnelles. C'est une lumière qui éclaire dans une seule direction ; c'est typiquement le cas du soleil (ou toute autre source très éloignée), dont tous les rayons nous arrivent (quasiment) parallèles :

Pour la décrire il nous suffit de donner sa direction, qui sera un vec3 normalisé (i.e. de longueur 1). On peut soit la mettre en constante dans le fragment shader const vec3 light_direction = normalize(vec3(0.2, 0.3, -1.));, soit la passer en uniform uniform vec3 light_direction; (ce qui est l'option la plus courante, car on veut pouvoir changer la direction de notre lumière sans avoir à recréer un nouveau shader à chaque fois).
Une fois que vous avez cette direction, pour mesurer à quel point notre triangle fait face à la lumière (et donc à quel point il est éclairé) nous allons utiliser le produit scalaire (dot(v1, v2) en glsl). Le produit scalaire entre deux vecteurs parfaitement alignés vaut 1 (si les vecteurs sont normalisés), il vaut -1 si les vecteurs sont parfaitement opposés, et il vaut 0 si les vecteurs sont orthogonaux. On peut ensuite multiplier la couleur de notre pixel par le résultat de ce produit scalaire (avec un signe moins), ce qui va nous donner un premier modèle d'éclairage simpliste : Quand la normale et la direction de la lumière sont parfaitement opposées c'est l'éclairage maximal, et on va multiplier par un produit scalaire qui vaut 1, donc conserver toute la couleur du pixel. À l'inverse quand les vecteurs sont perpendiculaires aucune lumière n'arrive sur notre surface, et ça correspond bien au fait de multiplier par un produit scalaire qui vaut 0 dans ce cas.

astuce

Pour nos produits scalaires on a besoin que les deux vecteurs soient normalisés, donc pensez bien à toujours normaliser vos normales !
Et attention, il y a des petits pièges : par exemple si vos normales sont normalisées dans le vertex shader, et qu'ensuite vous les passez au fragment shader via une variable in / out, elles ne seront plus normalisées, car l'interpolation entre les sommets se produit, et la moyenne de vecteurs normalisés n'est pas nécessairement normalisée.

Lumière ambiante

Un premier défaut qu'on peut tout de suite voir c'est que certaines parties du bateau sont complètement noires, car elles sont à l'opposé de la lumière. Ce n'est pas très réaliste, car dans la vraie vie même si on n'est pas directement exposé à la lumière celle-ci rebondit sur les objets environnants et vient éclairer un peu partout. C'est ce qui s'appelle de l'illumination globale. Il y a des techniques pour simuler ça dans les moteurs de jeu, mais ça devient assez complexe. Pour faire simple on peut juste rajouter un terme de lumière ambiante qui va faire une approximation de cette illumination globale. Il suffit d'additionner un petit quelque chose (0.3 par exemple) à notre produit scalaire, pour l'empêcher de tomber jusqu'à 0 (et aussi, si le produit scalaire devient négatif, il faut le limiter à 0, afin que notre +0.3 ait de l'effet dans toutes les zones noires, et pas seulement dans celles où le produit scalaire est > -0.3).

Lumière ponctuelle

Un autre type de lumière assez simple est la lumière ponctuelle. Elle est décrite par une position (vec3) et illumine de manière égale dans toutes les directions autour d'elle. C'est typiquement le cas des ampoules et autres petites sources de lumière.

Le calcul d'éclairage est le même que pour une lumière directionnelle. Mais il nous faut d'abord calculer la direction de la lumière, qui cette fois-ci dépend de la position du pixel concerné. Il faut donc récupérer la position dans le fragment shader, puis calculer le vecteur entre la position du pixel et la position de la lumière. De plus, l'intensité d'une lumière ponctuelle décroît à mesure qu'on s'en éloigne, donc il faut diviser le tout par la distance au carré¹.

astuce

Pour contrôler l'influence des différentes lumières, vous pouvez leur rajouter une intensité (a.k.a. un nombre que vous allez multiplier au résultat du produit scalaire) afin d'augmenter ou diminuer l'effet d'une lumière.

Normal Matrix et Model Matrix

Si on se met à appliquer une matrice modèle à notre objet, par exemple pour le faire tourner, on se rend compte d'un petit problème :

L'éclairage ne prend pas en compte la transformation de notre objet ! C'est comme si il ne tournait pas aux yeux de la lumière ! C'est parce que les positions et normales qu'on récupère depuis le vertex buffer sont exprimées en Object Space, alors que la position / direction de notre lumière est en World Space. Pour pouvoir faire nos calculs il faut que tout soit exprimé dans le même repère ! Pour convertir les positions et normales de nos pixels depuis l'Object Space vers le World Space, il faut leur appliquer la Model Matrix. Et je vous donne ces deux fonctions pour appliquer correctement une matrice à une position et à une direction en prenant bien en compte les coordonnées homogènes :

vec3 apply_matrix_to_position(mat4 matrix, vec3 point)
{
    vec4 tmp = matrix * vec4(point, 1.);
    return tmp.xyz / tmp.w;
}

vec3 apply_matrix_to_direction(mat4 matrix, vec3 direction)
{
    vec4 tmp = matrix * vec4(direction, 0.);
    return normalize(tmp.xyz);
}

astuce

Pour éviter toute confusion à l'avenir, je vous conseille de toujours ajouter un petit suffixe à vos variables de position et direction, pour bien indiquer dans quel espace elles sont exprimées : par exemple _os pour object space, _ws pour world space, _vs pour view space, etc.

layout(location = 0) in vec3 in_position_os;
uniform mat4 model_matrix;

out vec3 position_ws;
// ...

void main()
{
    // ...
    position_ws = apply_matrix_to_position(model_matrix, in_position_os);
    // ...
}

De plus, ce n'est pas tout à fait la Model Matrix qu'il faut appliquer aux normales, mais la Normal Matrix, qui est l'inverse de la transposée de la Model Matrix (glm::inverse(glm::transpose(model_matrix))). Ça revient au même dans la plupart des cas, mais si jamais il y a une scale non-uniforme dans votre model matrix, alors ça déformerait les normales et il faut passer par la Normal Matrix pour corriger ça.

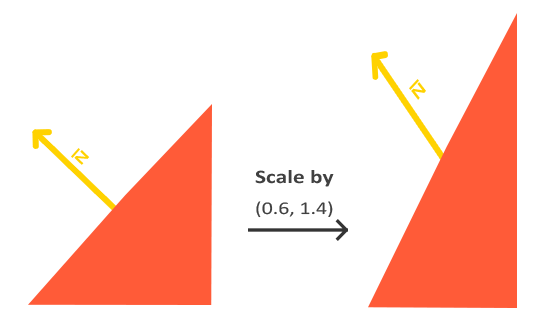
Normales incorrectement transformées par la Model Matrix

Si vous voulez savoir d'où vient la normal matrix et pourquoi c'est l'inverse de la transposée, je vous recommande ce petit article.

Lumières colorées

On peut aussi associer une couleur à chaque lumière, simplement en multipliant sa contribution par la couleur désirée (vec3) :

À vous de jouer !

Voici différents effets "avancés" que vous pouvez implémenter maintenant que vous connaissez les bases du rendu 3D !

Normal maps

Les normal maps permettent d'ajouter du détail à un mesh en modifiant la normale pour chaque pixel du triangle. Voici par exemple un tuto que vous pouvez suivre pour implémenter des normal maps. Et le même en version vidéo.

Ombres

Les shadow maps permettent de produire des ombres pour les lumières directionnelles. C'est le point de départ de toute une famille de technique plus raffinées, comme les omnidirectional shadow maps qui gèrent les lumières ponctuelles, et les cascaded shadow maps qui améliorent la qualité des ombres. Voici par exemple un tuto que vous pouvez suivre pour implémenter une shadow map basique. (Et vous verrez, c'est déjà un peu costaud !) Et le même tuto en version vidéo.

Effet see-through

Pour faire cette effet où on voit une silhouette des objets à travers les murs, il vous suffit, une fois toute la scène rendue normalement, de redessiner une deuxième fois l'objet sur lequel vous voulez appliquer l'effet, avec ce setup particulier :

• Appliquer un shader spécial qui va donner le visuel de la silhouette, par exemple retourner une couleur unie pour faire simple
• Changer le depth test, pour que l'objet ne s'affiche que si il est derrière d'autres objets. Je vous réfère à la documentation de glDepthFunc pour voir comment faire ça.

Matériaux et modèles d'éclairages plus avancés

Je vous réfère à ces tutos :

• Basic Lighting, il y a un peu de redite de ce qu'on a vu, mais aussi des nouveautés
• Materials
• Blinn-Phong
• PBR part 1
• PBR part 2

Footnotes

1. C'est dû au principe physique de conservation d'énergie : à un instant t la source émet une certaine quantité d'énergie, et cette énergie s'éloigne de la source, formant une sphère de plus en plus grande. Comme la même quantité d'énergie doit être présente sur une sphère de plus en plus grande, l'énergie en un point donné doit décroître proportionnellement à la surface de la sphère, soit $R^2$. ↩